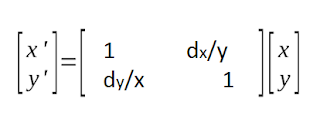Introdução à Computação Gráfica - UFPB

1. INTRODUÇÃO

O pipeline gráfico consiste exatamente de uma sequência de passos necessários para transformar uma descrição geométrica/matemática de uma cena 3D em uma descrição visual na tela 2D. A imagem final é obtida por meio da rasterização das primitivas projetadas na tela. Basicamente, cada passo do pipeline gráfico consiste de uma transformação geométrica de um sistema de coordenadas (espaço) para outro, são eles :

FIGURA 1 - Pipeline gráfico - imagem retirada das notas de aula do professor Christian.

Esta segunda parte do trabalho tem como objetivo implementar as transformações que levarão os vértices descritos no espaço objeto (object space) para o espaço da tela. A rasterização das primitivas será feita utilizando o código e o conhecimento da primeira parte do trabalho (Trabalho 1 : Rasterização de pontos e linhas ).

2. TRANSFORMAÇÕES AO LONGO DO PIPELINE GRÁFICO

As transformações ao longo do pipeline gráfico serão implementadas utilizando matrizes e coordenadas homogêneas.

2.1. Do Espaço Objeto (Object Space) para o Espaço do Universo (World Space)

O espaço objeto é o espaço onde cada objeto é criado e modelado a partir de suas primitivas geométricas utilizando seu próprio sistema de coordenadas.

A primeira etapa do pipeline consiste na passagem de vértices do espaço objeto para o espaço do universo. Essa passagem ocorre pela multiplicação de cada vértice por uma matriz de modelagem (model matrix), que consiste de uma combinação de uma ou mais transformações geométricas, que por sua vez também são representadas por matrizes.

FIGURA 2 - Pipeline gráfico - espaço objeto para o espaço do universo - imagem retirada das notas de aula do professor Christian.

As transformações geométricas são operações que visam a alteração de algumas características, como : posição, orientação, forma e/ou tamanho do objeto a ser desenhado. Elas podem ser representadas por equações, porém, a manipulação de objetos gráficos envolve muitas operações aritméticas, sendo assim, representá-las na forma de matriz facilitada o seu uso e entendimento. As principais transformações são :

Escala

Escalonar significa redimensionar um objeto, ou seja, aumentar ou diminuir suas dimensões, deformá-lo ou até mesmo espelhá-lo. Para fazer isso, basta multiplicar os valores das coordenadas de um vértice por um fator de escala - lembrando que as coordenadas de um vértice possuem valores inteiros para X, Y e Z no modelo 3D e para X e Y no modelo 2D. Essa operação de multiplicação deve ser feita para todos os vértices do objeto. Ao longo da postagem, vamos adotar a seguinte notação : vetor transformado = matriz de transformação x vetor original. Cada vetor é uma generalização para os vértices do objeto.

Matriz Escala 2D :

A escala pode ser isotrópica (quando os fatores de escala Sx e Sy são iguais) ou anisotrópica (quando os fatores de escala Sx e Sy são diferentes).

FIGURA 3 - Tipos de escalas - imagem retirada das notas de aula do professor Christian.

O espelhamento consiste em colocar o valor de Sx ou Sy para -1 ou 1 ou de ambos para -1.

FIGURA 4 - Espelhamento - imagem retirada das notas de aula do professor Christian.

Rotação

A rotação consiste em rotacionar os vértices de um objeto a partir de um ângulo dado. Se esse ângulo for positivo, a rotação ocorre no sentido anti-horário, porém, se o ângulo for negativo, a rotação ocorre no sentido horário. No espaço 2D, a rotação ocorre em torno da origem do sistema de coordenadas.Para criarmos a matriz de rotação, considere primeiramente um vetor w partindo da origem com posições x e y e formando um ângulo alfa com um eixo x. Em seguida, esse mesmo vetor sofre uma rotação de ângulo teta no sentido anti-horário e passa a ter novas posições x’ e y’. Aplicando relações de seno e cosseno e propriedades trigonométricas, conseguiremos calcular os valores de x’ e y’ a partir do ângulo teta e dos valores de x e y.

FIGURA 5 - Rotação do longo da origem - imagens retiradas das notas de aula do professor Christian.

FIGURA 6 - Rotação na origem e fora da origem - imagem retirada das notas de aula do professor Christian.

Matriz Rotação 2D :

Translação

Transladar consiste em movimentar os vértices de um objeto adicionando quantidades às suas coordenadas, ou seja, cada ponto pode ser movido por d unidades ao longo de cada eixo do sistema de coordenadas. Se fôssemos escrever uma matriz seguindo as mesmas regras de construção das matrizes acima, ele ficaria assim:

x’ = x + dx

y’ = y + dy

Notou algo de diferente na matriz acima ? Caso não tenha notado, perceba que x e y estão inseridos na matriz. E qual o problema nisso ? O problema é que em vez de criarmos uma matriz única para todos os vértices do objeto (como estamos fazendo até agora), com a matriz dessa forma teremos que escrever uma matriz para cada vértice do meu objeto, ou seja, se um objeto tiver 10 vértices criaremos então 10 matrizes. Em geral, uma cena ou um objeto contém milhares de vértices, o que acarretaria em milhares de matrizes, aumentando assim o custo computacional e prejudicando no desempenho da aplicação.

Porém, uma solução seria criarmos uma matriz translação utilizando coordenadas homogêneas, isso significa que o tamanho do vetor terá um acréscimo de uma dimensão, ou seja, os vetores serão representados por n+1 coordenadas, por exemplo, (X,Y) passará a ser (X,Y,W). Se quisermos transformar de Coordenadas Homogêneas para o Espaço Euclidiano, basta dividir as coordenadas X e Y pela homogênea W. Fazer essa alteração é bom e importante, pois podemos também representar as demais transformações por meio de coordenadas homogêneas e combiná-las para dar origem a uma matriz única (como veremos mais à frente). A coordenada homogênea pode assumir quaisquer valores inteiros, inclusive zero, mas apenas utilizaremos seu valor como sendo 1. Logo, a representação matricial para a translação seria :

FIGURA 7 - Matriz de translação - imagens retiradas das notas de aula do professor Christian.

Shear

Uma outra forma de deformar os objetos de uma cena seria aplicando esta transformação. O shear mantém uma coordenada U fixa enquanto muda a coordenada V ao longo de seu eixo, ou seja, há uma relação linear entre V e U.

FIGURA 8 - Shear em X - imagem retirada das notas de aula do professor Christian.

Porém, a maioria das APIs gráficas atuais não implementam o shear diretamente. E como elas fazem ? O shear é simulado por uma combinação de uma rotação, uma escala e uma outra rotação. Este trabalho não implementa em código a transformação shear.

FIGURA 9 - Simulação do shear em X - imagem retirada das notas de aula do professor Christian.

Espaço 3D

Perceba que as matrizes acima foram modeladas para o espaço 2D. Como ficariam essas transformações no espaço 3D ? Bem simples ! As matrizes em 3D para as transformações acima e já com coordenadas homogêneas ficariam :

Matriz Escala 3D e com coordenadas homogêneas :

Matriz Rotação 3D ao longo do eixo X e com coordenadas homogêneas :

Matriz Rotação 3D ao longo do eixo Y e com coordenadas homogêneas :

Matriz Rotação 3D ao longo do eixo Z e com coordenadas homogêneas :

Matriz Translação 3D e com coordenadas homogêneas :

Matriz Shear 3D com coordenadas homogêneas :

O exemplo do shear acima altera X e Y pelos valores proporcionais a Z, sendo assim, essa é apenas uma das matrizes shear que podem ser geradas trocando apenas a posição do fator de shear ‘m’ ao longo da matriz. Esse exemplo serve apenas para mostrar que é possível gerar matrizes no espaço 3D, mas não foca nos casos possíveis e nos detalhes da transformação em si. Note também que, diferentemente do espaço 2D, a rotação no espaço em 3D não ocorre ao longo da origem, mas sim ao longo de cada eixo do sistema de coordenadas.

Ah ! Lembra da matriz de modelagem ? Aquela matriz model. Pois é, já ia me esquecendo … As matrizes vistas acima combinadas darão origem à model. Isso mesmo ! A matriz model é nada mais nada menos que a multiplicação das matrizes acima em uma ordem pré-estabelecida e é ela que é responsável por levar os vértices dos objetos do espaço objeto para o espaço do universo.

Matriz model = Matriz de transformação 1 + Matriz de transformação 2 + …+ Matriz de transformação n

Bem, após ver toda essa teoria, como ficaria tudo isso implementado em código ? Todo código deste trabalho foi feito utilizando as linguagens de programação C/C++ e as bibliotecas GLM e OpenGL. O trecho de código a seguir implementa as matrizes acima :

FIGURA 10 - Trecho de código escrito em C/C++.

2.2. Do Espaço do Universo (World Space) para o Espaço da Câmera (Camera Space)

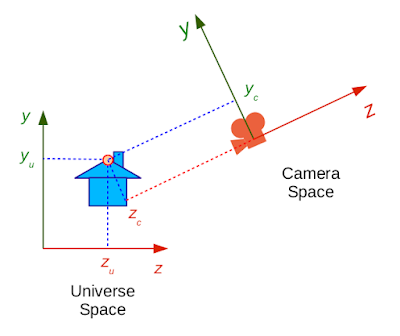
Até agora vimos que podemos modelar objetos num espaço próprio (espaço objeto) e “jogá-los” no espaço universo. E agora, o que faremos ? A segunda etapa do pipeline gráfico consiste justamente em levar os objetos do espaço universo para o espaço da câmera. Como será feito ? Primeiro, precisamos colocar a nossa câmera em algum ponto do espaço universo. Só isso ? Não. Precisamos também de um up, ou seja, um vetor que fixe a câmera no espaço. Além disso, precisamos de um vetor direção que aponte para onde a câmera está olhando. Porém, às vezes é mais fácil definirmos um ponto para o qual a câmera esteja olhando e, junto com a posição da câmera, calcular o vetor direção fazendo a subtração entre a posição da câmera e do ponto para o qual ela olha.

FIGURA 11 - Espaço do universo e espaço da câmera - imagem retirada das notas de aula do professor Christian.

FIGURA 12 - Pipeline gráfico - espaço objeto, espaço do universo e espaço da câmera - imagem retirada das notas de aula do professor Christian.

Após definir os três elementos acima (up, vetor direção e posição da câmera), iremos criar um novo sistema de coordenadas para o espaço da câmera, ou seja, precisamos definir também os eixos X, Y e Z (já que estamos utilizando objetos quaisquer em 3D). Para isso, utilizaremos produtos vetoriais e normalização de vetores.

FIGURA 13 - Criando os eixos do sistema de coordenadas da câmera - imagem retirada das notas de aula do professor Christian.

Note pela fórmula acima que, o eixo Z é oposto ao vetor direção; os eixos são perpendiculares entre si, ou seja, formam ângulos de 90 graus (são ortogonais) e a base do sistema de coordenadas é ortonormal - possuem comprimento 1.Já definimos o up, o vetor direção e a posição da câmera. Já calculamos também os eixos X, Y e Z, agora só falta definirmos uma matriz, assim como foi feito na primeira etapa, que leve os vértices do espaço universo para o espaço da câmera. Essa matriz é chamada matriz de visualização (view matrix) que é uma combinação de uma translação e uma rotação.

FIGURA 14 - Matriz view - imagens retiradas das notas de aula do professor Christian.

A matriz da esquerda é a matriz de rotação. Ela contém as componentes dos três eixos. Já a matriz da direita, a matriz de translação, contém a posição da câmera com valores opostos. Em código, essa mesma matriz view é implementada da seguinte maneira:

FIGURA 15 - Trecho de código escrito em C/C++.

A matriz view e a matriz model podem ser combinadas para formar uma única matriz (a matriz modelview):

M_Model_View = M_View * M_Model

2.3. Do Espaço da Câmera (Camera Space) para o Espaço de Recorte ou Projetivo (Clipping Space)

Até agora já percorremos metade do pipeline gráfico. Esta terceira etapa consiste em transformar vértices do espaço da câmera para o espaço de recorte (ou projetivo) e mais uma vez iremos construir uma matriz, a matriz de projeção (projection matrix). Dada a seguinte situação :

FIGURA 16 - Relação trigonométrica - Semelhança de triângulos - imagem retirada das notas de aula do professor Christian.

Considerando que estamos no espaço da câmera, o ponto ‘p’ da figura acima representa um vértice genérico de um objeto no espaço da câmera. Esse ponto é projetado sobre um plano (o view plane) que, inicialmente, coincide com o eixo Y gerando um p’ que contém um y’ como coordenada. O ponto ‘c’ é o ponto onde está localizada a câmera. E por que a câmera não está na origem como deveria ser ? Inicialmente, a câmera não ficará na origem do sistema para facilitar a construção matemática e o entendimento do problema. O ‘d’ representa a distância entre a câmera e o view plane. Tendo todas essas informações em mente, perceba que podemos realizar uma manipulação trigonométrica utilizando semelhança de triângulos e com isso obteremos uma relação para y’. Da mesma forma faremos para x’. Bem, nosso objetivo final é representar uma cena 3D em uma tela 2D, lembra ? Você poderia pensar : se eu já tenho uma relação para x’ e outra para y ‘, agora só preciso fazer z’ igual a zero, não ? É, caso você tenha pensado assim, seu pensamento está errado, pois se z’ = 0 perderíamos a informação de profundidade dos objetos. Uma solução seria fazer z’ = z e com isso preservaríamos a informação de profundidade, porém, vamos representar z’ de forma semelhante a x’ e y’ e com isso podemos gerar uma matriz utilizando coordenadas homogêneas. Vale ressaltar que z’ mantém a ordem dos pontos ao longo do eixo (relação de ordem).

FIGURA 17 - Relação trigonométrica - Semelhança de triângulos - imagem retirada das notas de aula do professor Christian.

Antes do ponto P (x,y,z,w,1) se transformar para P’(x’,y’,z’,1), no espaço de recorte ele é P’p (x,y,z,1-z/d), ou seja, nesta etapa do pipeline gráfico o valor da coordenada homogênea w é diferente de 1. A matriz de projeção leva um ponto P (x,y,z,w,1) do espaço da câmera para um ponto P’p (x,y,z,1-z/d) no espaço de recorte e é escrita da seguinte maneira:

Na prática, a câmera coincide com a origem e o view plane dista ‘d’ unidades do eixo Y, como na figura abaixo:

FIGURA 18 - Relação trigonométrica - Semelhança de triângulos - imagem retirada das notas de aula do professor Christian.

Para isso, precisamos de uma outra matriz, uma matriz de translação Mt.

Logo, a matriz de projeção será a combinação das matrizes Mp e Mt.

FIGURA 19 - Matriz de projeção - imagem retirada das notas de aula do professor Christian.

FIGURA 20 - Trecho de código escrito em C/C++.

A matriz modelview e a matriz projection podem ser combinadas para formar uma única matriz:

M_Model_View_Projection = M_Projection * M_Model_View

2.4. Do Espaço de Recorte ou Projetivo (Clipping Space) para o Espaço Canônico (Canonical Space)

Esta etapa do pipeline é responsável por transformar vértices do espaço de recorte para o espaço canônico. Primeiro, iremos dividir as coordenadas dos vértices (pontos) no espaço de recorte P’p (x,y,z,1-z/d) pela sua coordenada homogênea w (processo conhecido como homogeneização), gerando assim um ponto P’ (x’,y’,z’,1). A divisão de w por ele mesmo faz com que ele retorne a ter valor 1. Fazendo essa divisão por w, definitivamente, estaremos aplicando a distorção não linear dos objetos - tornando menores os objetos distantes da câmera e maiores os que estiverem próximos da câmera.

Junto a isso, há um mapeamento de um volume de visualização (view frustum), com formato de um hexaedro que posteriormente é transformado em um cubo de coordenadas unitárias e centrado na origem. Esse cubo é espaço canônico, onde o que estiver dentro dele é visível. As matrizes apresentadas acima são didáticas e, por conta disso, não permitem a geração de um cubo perfeito, porém, é gerado um volume bastante similar a um cubo.

FIGURA 21 - Distorção dos objetos após a homogeneização - imagem retirada das notas de aula do professor Christian.

2.5. Do Espaço Canônico (Canonical Space) para o Espaço de Tela (Screen)

Esta penúltima etapa do pipeline gráfico é responsável por transformar vértices do espaço canônico para o espaço de tela. Na verdade, o que iremos fazer é um mapeamento de cada vértice para a tela, uma vez que estão em sistema de coordenadas diferentes - na tela, a origem do sistema de coordenadas fica localizado no canto superior esquerdo e eixo Y cresce positivamente de cima para baixo.

FIGURA 22 - Mapeamento do espaço canônico para o espaço da tela.

O mapeamento será feito por meio da multiplicação de cada vértice por uma matriz que envolve escalas e translações, como pode ser visto abaixo :

Na matriz, o ‘w’ representa o largura (comprimento) da tela e ‘h’ representa a altura da tela.

FIGURA 23 - Trecho de código escrito em C/C++.

A última etapa consiste justamente em rasterizar os vértices que foram passados ao longo de todo pipeline gráfico. Toda teoria de rasterização de primitivas geométricas pode ser visto melhor na postagem abaixo (Trabalho 1 : Rasterização de pontos e linhas). Após percorrer todo o pipeline gráfico e passar pelo processo de rasterização, o resultado será um frame de uma cena ou um objeto em particular.

3. RESULTADOS

Toda teoria vista acima serve para desenhar qualquer objeto tridimensional na tela bidimensional. Vamos ver se funciona ? Melhor ainda ! Vamos comparar os resultados do mesmo objeto sendo desenhado por uma aplicação equivalente escrita em OpenGL. Utilizarei um objeto já criado pelo software (programa) de modelagem Blender, mas nada impede que você mesmo modele seu próprio objeto ou cenário.

Vídeo comparativo

Para efeito de comparação, utilizei o conteúdo de um arquivo .obj. O objeto escolhido foi a macaquinha Suzanne do próprio Blender. Tanto o programa que implementa as matrizes acima quanto o seu equivalente em OpenGL carregam os vértices do objeto e desenha-o na tela. A primeira tela corresponde ao programa em OpenGL e a segunda o programa implementado com matrizes e coordenadas homogêneas.

FIGURA 24 - Teste comparativo - programas em execução.

FIGURA 25 - Teste comparativo - programas em execução.

FIGURA 26 - Teste comparativo com outros objetos - programas em execução.